Salvini analizza Oreo | La Voce News
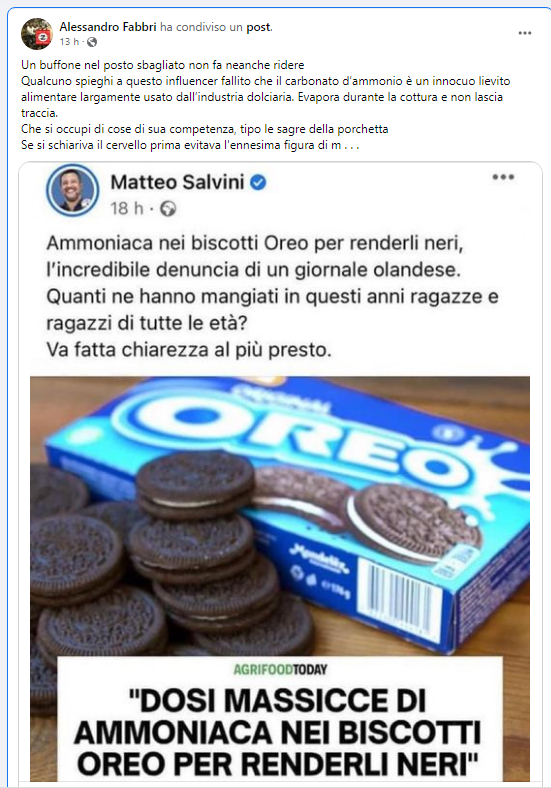
Dosi massicce di ammoniaca nei biscotti Oreo" LA DENUNCIA CHOC! Salvini: «Va fatta chiarezza» - YouTube
Ammoniaca nei biscotti Oreo", perché il tweet di Matteo Salvini non ci deve allarmare
Biscotti OREO 'pieni zeppi di Ammoniaca', lo scandalo che sta investendo il famoso marchio
Perché Salvini sugli Oreo attacca il made in Italy (senza volerlo)
Perché non convince l'accusa di usare ammoniaca nel cacao degli Oreo | il Salvagente
Ammoniaca negli Oreo: l'azienda fa chiarezza
Ammoniaca nei biscotti oreo: l'azienda fa chiarezza e risponde alle accuse di Salvini
Ammoniaca negli Oreo: l'azienda fa un comunicato; vi sveliamo cosa ha detto, gli aggiornamenti
Biscotti Oreo: sai perché sono così scuri? "Viene aggiunta ammoniaca tossica al cacao", l'inchiesta olandese - greenMe
Ammoniaca e allarmismo | Butac - Bufale Un Tanto Al Chilo
Biscotti Oreo e l'inchiesta shock olandese: 'Troppa ammoniaca per renderli così neri'
Ammoniaca negli Oreo, l'azienda: "nessun rischio" - IL MONDO
Oreo: ti spieghiamo perché l'ammoniaca utilizzata per trattare il cacao non è pericolosa per la nostra salute - greenMe
Ammoniaca nei biscotti Oreo scoperta in un'azienda in Olanda: sul caso interviene Salvini | LA NOTIZIA
Cacao trattato con ammoniaca nei biscotti Oreo? La rivelazione shock di un quotidiano olandese - VALDARNO INFORMA
Biscotti Oreo all'ammoniaca? Nessun rischio per la salute – Query Online
Oreo, la verità sull'inchiesta che rivela la presenza di ammoniaca nei biscotti | Notizie da TeleAmbiente TV News
Cos'è una notizia? A proposito di ammoniaca e biscotti Oreo - L'INDIPENDENTE
Dosi massicce di ammoniaca nei biscotti Oreo per renderli neri"
Matteo Salvini on X: "Ammoniaca nei biscotti Oreo per renderli neri, l'incredibile denuncia di un giornale olandese. Quanti ne hanno mangiati in questi anni ragazze e ragazzi di tutte le età? Va
Oreo, scandalo in Olanda: nei biscotti ci sarebbe davvero troppa ammoniaca
Biscotti Oreo mischiati con l'ammoniaca, la denuncia choc. Salvini: «Va fatta chiarezza»
A quanto pare i biscotti Oreo sono pieni di ammoniaca - L'INDIPENDENTE
