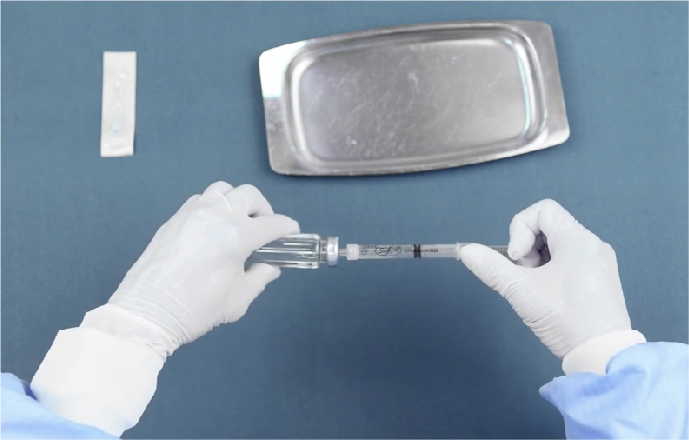
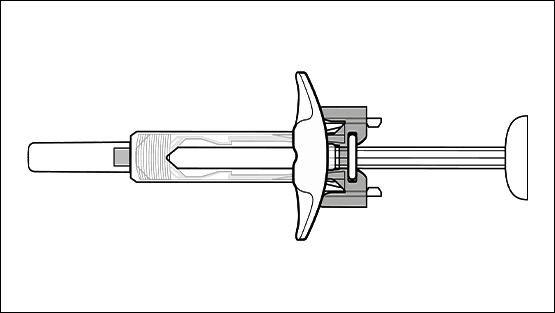
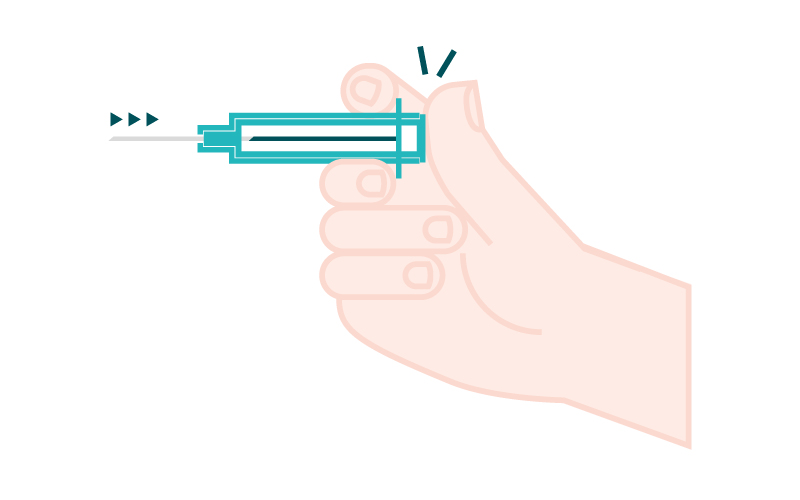
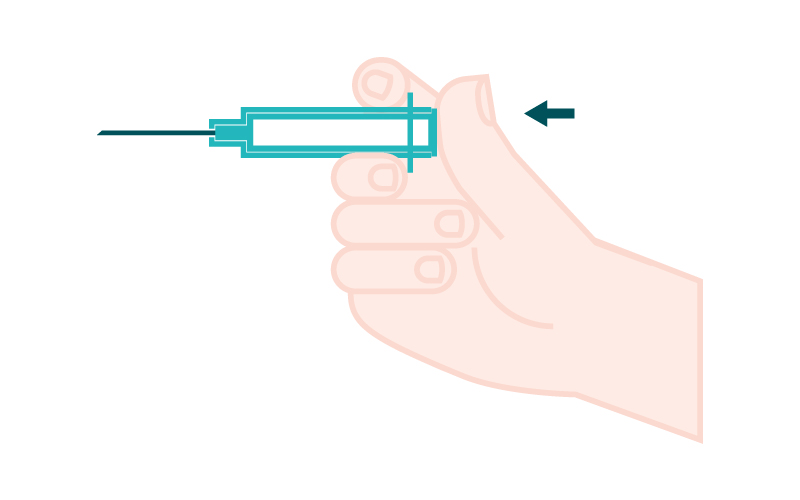
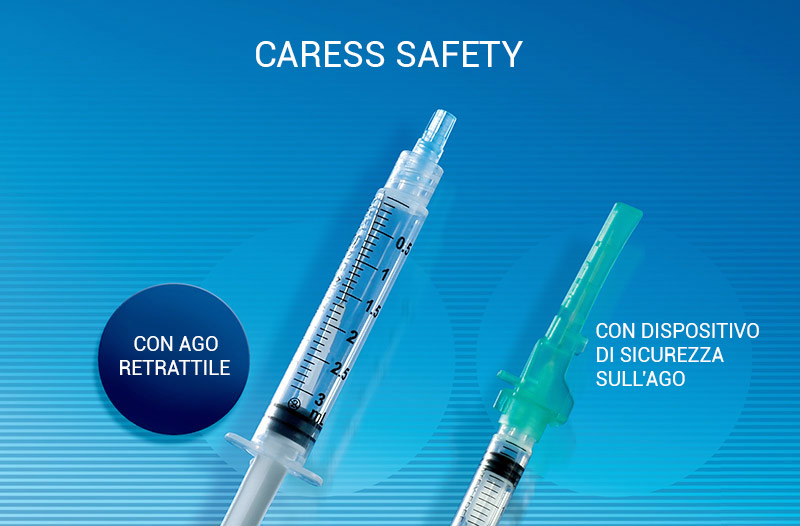
Siringa di sicurezza cinese con ago retrattile automatico Produttori, fornitori, fabbrica - Made in China - Pingan
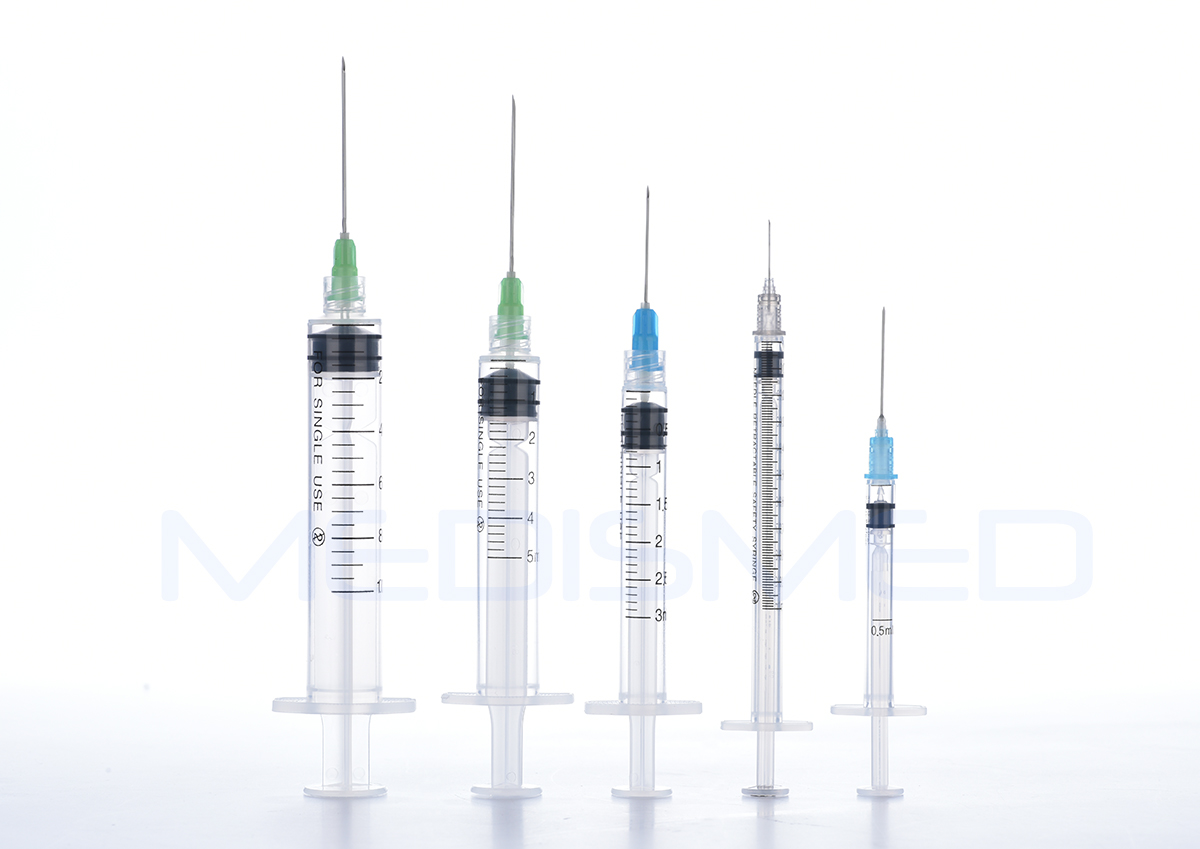
Siringhe Di Sicurezza Retrattili Con Ago Medis – Siringhe usa e getta Fornitori di Medrad Liebel Flarsheim Nemoto Medtron CT | MRI | ANGIO | Iniettori di mezzi di Contrasto CATH LAB

Cina Siringa di sicurezza da 10 ml con ago retrattile automatico Produttori, fornitori, fabbrica - Made in China - Pingan